จำนวนเชิงซ้อนใด ๆ สามารถเขียนเป็นกราฟได้บนระนาบที่เรียกว่า ระนาบเชิงซ้อน ซึ่งประกอบด้วย 2 แกน คือ
| |
1. แกนนอน |
เรียกว่า แกนจริง |
| |
2. แกนตั้ง |
เรียกว่า แกนจินตภาพ |
| |
กำหนดให้ |
z |
= |
a + bi |
| |
สามารถเขียน z ในรูปคู่อันดับ ได้เป็น |
| |
|
z |
= |
(a, b) |
| |
จะได้กราฟของ z บนระนาบเชิงซ้อนดังนี้ |
ในการเขียนกราฟของจำนวนเชิงซ้อน z = a + bi อาจทำได้โดย
| |
1. วาดจุดลงบนระนาบเชิงซ้อนที่พิกัด (a, b) |
| |
2. วาดเวกเตอร์ที่มีจุดเริ่มต้นที่พิกัด (0, 0) และจุดสิ้นสุดที่พิกัด (a, b) |
| |
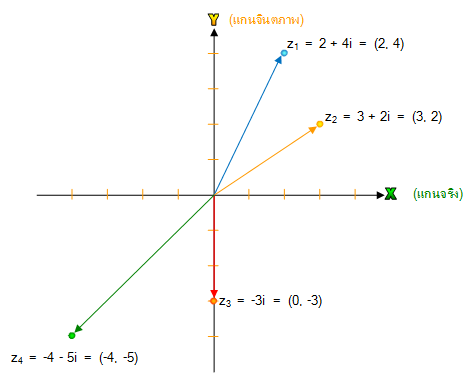
จงเขียนกราฟของจำนวนเชิงซ้อนที่กำหนดให้ต่อไปนี้
| 1. z1 = 2 + 4i |
2. z2 = 3 + 2i |
3. z3 = 3i |
4. z4 = -4 - 5i |
|
|
| |
จากจำนวนเชิงซ้อนที่กำหนดให้ สามารถเขียนในรูปคู่อันดับได้ดังนี้ |
| |
| z1 |
= |
2 + 4i |
= |
(2, 4) |
| z2 |
= |
3 + 2i |
= |
(3, 2) |
| z3 |
= |
3i |
= |
(0, 3) |
| z4 |
= |
-4 - 5i |
= |
(-4, -5) |
|
| |
จากคู่อันดับที่ได้ สามารถเขียนเป็นกราฟได้ดังนี้ |
| |
 |
|

|
|
|