การพับกระดาษกับการประยุกต์
|
คณิตศาสตร์
เมื่อคลี่ Origami ที่พับแล้วออกมาดู จะพบกับลวดลายกระดาษที่พับเป็นลายพิมพ์เขียวไว้ ซึ่งลายเหล่านี้มีความเกี่ยวข้องกับรูปทรงที่พับออกมา เราสามารถใช้ความรู้คณิตศาสตร์ด้านเรขาคณิต มาประยุกต์กับการพับOrigamiได้
เรขาคณิตที่ใช้ในการทำOrigamiนี้ ถูกศึกษาโดย นักพับกระดาษ นักคณิตศาสตร์ นักวิทยาศาสตร์ และ ศิลปินหลายท่าน ตั้งแต่นักคณิตศาสตร์ชาวญี่ปุ่นเชื้อสายอิตาลี Humiaki Huzita ที่ได้คิดสูตรอธิบายความสัมพันธ์ของOrigamiกับเรขาคณิต, Jun Maekawa นักฟิสิกส์ที่คิดค้นทฤษฎีเกี่ยวกับOrigami และใช้มันในการออกแบบรูปทรงOrigamiต่างๆที่น่าตื่นตาตื่นใจมาก, นักคณิตศาสตร์ Toshikazu Kawasaki ที่คิดค้นทฤษฎีอีกหลายทฤษฎีเช่นกัน ซึ่งอธิบายถึงมิติที่4ของOrigamiด้วย Robert Lang ชาวอเมริกันที่พัฒนาการออกแบบOrigami โดยใช้คอมพิวเตอร์เข้ามาช่วย ทำให้ได้รูปทรงที่ซับซ้อนมากมาย นักวิชาการ Shuzo Fujimoto และศิลปิน Chris Palmer ที่ได้ค้นพบความเกี่ยวข้องระหว่างOrigamiและลายที่คล้ายการปูกระเบื้องโมเสส นอกจากนี้ยังมีครูอาจารย์หลายท่านที่ให้ความสนใจกับOrigamiและใช้มันเป็นสื่อการสอนวิชาต่างๆ เช่น คณิตศาสตร์, เคมี, ฟิสิกส์ และ สถาปนิกด้วย

รูปภาพจาก : http://www.origami
-cdo.it/articoli/img/huzita.jpg
|
Humiaki Huzita : กฎของ “Huzita-Hatori axioms”
สิ่งที่เขาอธิบายเรียกว่า “กฎของHuzitaและHatori” หรือ “กฎของ Huzita และ Justin” ซึ่งกล่าวถึงวิธีที่แตกต่างกัน 6 วิธีในการสร้างรอยพับจากเส้น และ จุดบนกระดาษ ซึ่งวิธีที่ 7ถูกค้นพบโดย Koshiro Hatori, Jacques Justin และ Robert J.Lang ในเวลาต่อมา |

รูปภาพจาก : http://www.
papercrane.org/attendees/
JunMaekawa/portrait.jpg |
Jun Maekawa : “ทฤษฎีบท Maekawa”
Jun Maekawa ได้รับการยกย่องเกี่ยวกับการสร้างOrigamiแบบใหม่
โดยใช้เรขาคณิตเข้ามาช่วย โดยเขาได้เชื่อมโยงความเกี่ยวข้องระหว่างคณิตศาสตร์กับOrigami และตั้งเป็น “ทฎษฎีบทของMaekawa”
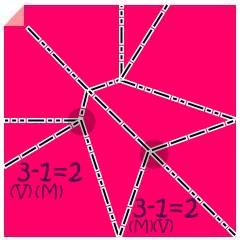
ถ้ากำหนดให้ M แทนจำนวนเส้นรอยพับแบบภูเขา
V แทนจำนวนเส้นรอยพับแบบหุบเขา
จะได้ว่า เมื่อนับรอบๆจุดตัดของเส้นต่างๆที่เกิดจากการพับ
แล้วกางออกเป็นแผ่นแบนๆ(flat vertex fold) นั้น จะพบว่า
M – V = 2 or V – M = 2
หรือพูดง่ายๆว่า ผลต่างของจำนวนเส้นรอยพับแบบภูเขา และ จำนวนเส้นรอยพับแบบหุบเขา เป็น 2 เสมอ
ตัวอย่าง
|
Toshikazu Kawasaki : ทฤษฎีบทของ Kawasaki
Toshikazu Kawasaki เป็นนักคณิตศาสตร์ ซึ่งรู้จักกันดีจากทฤษฎีการพับเครื่องบิน, การพับแบบมีมิติที่4 และการพับกุหลาบแบบKawasakiของเขา
ทฤษฎีบทของ Kawasaki บอกว่า รอยพับที่สามารถพับให้เกิดflat origamiจะต้องมีคุณสมบัติ คือ มีมุมรอบๆจุดที่เกิดจากการตัดกันของรอยพับ(Vertex)ซึ่ง กำหนดให้เป็น 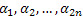 มีคุณสมบัติ คือ มีคุณสมบัติ คือ
สังเกตว่า จำนวนของมุมทั้งหมดเป็นเลขคู่เสมอ
ทฤษฎีบทของเขาสามารถอธิบายได้ง่ายๆ คือ ผลบวกของมุมเว้นมุม มีค่าเท่ากับ 180 องศา
- ReferenceFinder
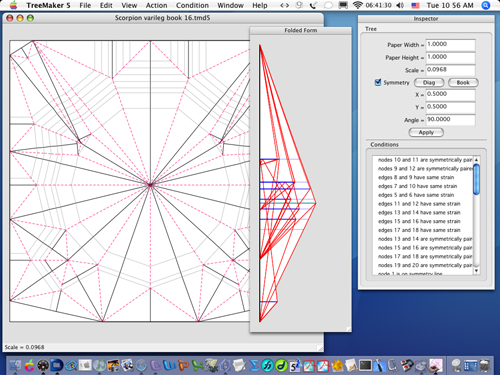
- TreemakerTreemaker
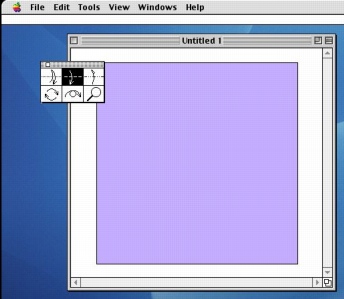
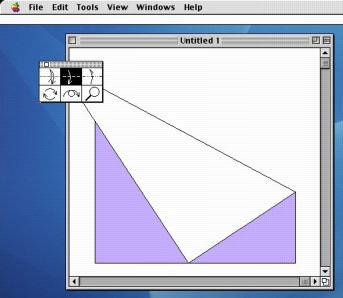
- Origami Simulation
ที่มา : http://kahuna.merrimack.edu/~thull/origamimath.html
http://www.langorigami.com
http://kahuna.merrimack.edu/~thull/combgeom/flatfold/flat.html
http://mathworld.wolfram.com/KawasakisTheorem.html
http://update.se-ed.com/265/origami-barking-dog-265.pdf
|